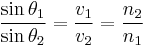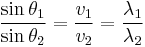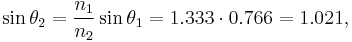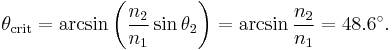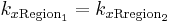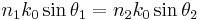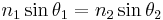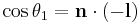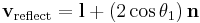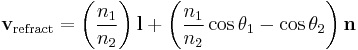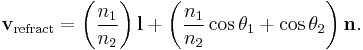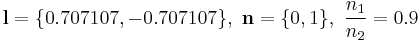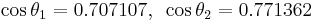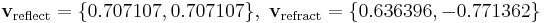Snell's law

In optics and physics, Snell's law (also known as Descartes' law, the Snell–Descartes law, and the law of refraction) is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass. The law says that the ratio of the sines of the angles of incidence and of refraction is a constant that depends on the media.

In optics, the law is used in ray tracing to compute the angles of incidence or refraction, and in experimental optics and gemology to find the refractive index of a material.

Refraction of light at the interface between two media of different refractive indices, with n₂ > n₁. Since the velocity is lower in the second medium (v₂ < v₁), the angle of refraction θ₂ is less than the angle of incidence θ₁; that is, the ray in the higher-index medium is closer to the normal.

Snell's law is also satisfied in the metamaterials which allow light to be bent "backward" at a negative index, with a negative angle of refraction.

Named after Dutch mathematician Willebrord Snellius, one of its discoverers, Snell's law states that the ratio of the sines of the angles of incidence and refraction is equivalent to the ratio of velocities in the two media, or equivalent to the opposite ratio of the indices of refraction:

$\frac{\sin\theta_1}{\sin\theta_2} = \frac{v_1}{v_2} = \frac{n_2}{n_1}$

v = velocity, SI units are m/s

n = refractive index, which is unitless

Snell's law follows from Fermat's principle of least time, which in turn follows from the propagation of light as waves.

1 History
2 Explanation
- 2.1 Total internal reflection and critical angle
- 2.2 Derivations
3 Vector form
4 Dispersion
5 See also
6 References
7 External links

History

Reproduction of a page of Ibn Sahl's manuscript showing his discovery of the law of refraction.

Ptolemy, a Greek living in Alexandria,^[1] had found a relationship regarding refraction angles, but it was inaccurate for angles that were not small. Ptolemy was confident he had found an accurate empirical law, partially as a result of fudging his data to fit theory (see: confirmation bias).^[2] Alhazen, in his Book of Optics (1021), came closer to discovering the law of refraction, though he did not take this step.^[3]

An 1837 view of the history of "the Law of the Sines"^[4]

The law of refraction was first accurately described by Ibn Sahl, of Baghdad, in the manuscript On Burning Mirrors and Lenses (984).^[5]^[6] He made use of it to work out the shapes of lenses that focus light with no geometric aberrations, known as anaclastic lenses.^[7]

Snell's law was discovered by Thomas Harriot in 1602,^[8] who however did not publish his results although he had corresponded with Kepler on this very subject.

In 1621, Willebrord Snellius (Snel) derived a mathematically equivalent form, that remained unpublished during his lifetime. René Descartes independently derived the law using heuristic momentum conservation arguments in terms of sines in his 1637 treatise Discourse on Method, and used it to solve a range of optical problems. Rejecting Descartes' solution, Pierre de Fermat arrived at the same solution based solely on his principle of least time.

According to Dijksterhuis,^[9] "In De natura lucis et proprietate (1662) Isaac Vossius said that Descartes had seen Snell's paper and concocted his own proof. We now know this charge to be undeserved but it has been adopted many times since." Both Fermat and Huygens repeated this accusation that Descartes had copied Snell.

In French, Snell's Law is called "la loi de Descartes" or "loi de Snell-Descartes."

Christiaan Huygens' construction

In his 1678 Traité de la Lumiere, Christiaan Huygens showed how Snell's law of sines could be explained by, or derived from, the wave nature of light, using what we have come to call the Huygens–Fresnel principle.

Although he spelled his name "Snel", as noted above, it has conventionally been spelled "Snell" in English, apparently by misinterpreting the Latin form of his name, "Snellius".^[10]

Explanation

Snell's law is used to determine the direction of light rays through refractive media with varying indices of refraction. The indices of refraction of the media, labeled $n_1$ , $n_2$ and so on, are used to represent the factor by which a light ray's speed decreases when traveling through a refractive medium, such as glass or water, as opposed ^[11] to its velocity in a vacuum.

As light passes the border between media, depending upon the relative refractive indices of the two media, the light will either be refracted to a lesser angle, or a greater one. These angles are measured with respect to the normal line, represented perpendicular to the boundary. In the case of light traveling from air into water, light would be refracted towards the normal line, because the light is slowed down in water; light traveling from water to air would refract away from the normal line.

Refraction between two surfaces is also referred to as reversible because if all conditions were identical, the angles would be the same for light propagating in the opposite direction.

Snell's law is generally true only for isotropic or specular media (such as glass). In anisotropic media such as some crystals, birefringence may split the refracted ray into two rays, the ordinary or o-ray which follows Snell's law, and the other extraordinary or e-ray which may not be co-planar with the incident ray.

When the light or other wave involved is monochromatic, that is, of a single frequency, Snell's law can also be expressed in terms of a ratio of wavelengths in the two media, λ₁ and λ₂:

$\frac{\sin\theta_1}{\sin\theta_2} = \frac{v_1}{v_2} = \frac{\lambda_1}{\lambda_2}$

Total internal reflection and critical angle

Demonstration of no refraction at angles greater than the critical angle.

When light travels from a medium with a higher refractive index to one with a lower refractive index, Snell's law seems to require in some cases (whenever the angle of incidence is large enough) that the sine of the angle of refraction be greater than one. This of course is impossible, and the light in such cases is completely reflected by the boundary, a phenomenon known as total internal reflection. The largest possible angle of incidence which still results in a refracted ray is called the critical angle; in this case the refracted ray travels along the boundary between the two media.

For example, consider a ray of light moving from water to air with an angle of incidence of 50°. The refractive indices of water and air are approximately 1.333 and 1, respectively, so Snell's law gives us the relation

$\sin\theta_2 = \frac{n_1}{n_2}\sin\theta_1 = 1.333 \cdot 0.766 = 1.021,$

which is impossible to satisfy. The critical angle θ_crit is the value of θ₁ for which θ₂ equals 90°:

$\theta_\text{crit} = \arcsin\left(\frac{n_2}{n_1}\sin\theta_2\right) = \arcsin\frac{n_2}{n_1} = 48.6^\circ.$

Derivations

Wavefronts from a point source in the context of Snell's law. The region below the grey line has a higher index of refraction, and proportionally lower speed of light, than the region above it.

Snell's law may be derived from Fermat's principle, which states that the light travels the path which takes the least time. By taking the derivative of the optical path length, the stationary point is found giving the path taken by the light (though it should be noted that the result does not show light taking the least time path, but rather one that is stationary with respect to small variations as there are cases where light actually takes the greatest time path, as in a spherical mirror). In a classic analogy, the area of lower refractive index is replaced by a beach, the area of higher refractive index by the sea, and the fastest way for a rescuer on the beach to get to a drowning person in the sea is to run along a path that follows Snell's law.

Alternatively, Snell's law can be derived using interference of all possible paths of light wave from source to observer—it results in destructive interference everywhere except extrema of phase (where interference is constructive)—which become actual paths.

Another way to derive Snell’s Law involves an application of the general boundary conditions of Maxwell equations for electromagnetic radiation.

Yet another way to derive Snell's law is based on translation symmetry considerations.^[12] For example, a homogeneous surface perpendicular to the z direction can not change the transverse momentum. Since the propagation vector 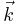$\vec{k}$ is proportional to the photon's momentum, the transverse propagation direction 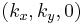$(k_x,k_y,0)$ must remain the same in both regions. 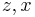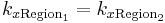Assuming without loss of generality a plane of incidence in the $z,x$ plane $k_{x\text{Region}_1} = k_{x\text{Region}_2}$ . Using the well known dependence of the wave number on the refractive index of the medium, we derive Snell's law immediately.

$k_{x\text{Region}_1} = k_{x\text{Rregion}_2} \,$

$n_1 k_0\sin\theta_1 = n_2 k_0\sin\theta_2 \,$

$n_1\sin\theta_1 = n_2\sin\theta_2 \,$

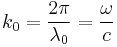where $k_0=\frac{2\pi}{\lambda_0}=\frac{\omega}{c}$ is the wavenumber in vacuum. Note that no surface is truly homogeneous, in the least at the atomic scale. Yet full translational symmetry is an excellent approximation whenever the region is homogeneous on the scale of the light wavelength.

Vector form

Given a normalized light vector l (pointing from the light source toward the surface) and a normalized plane normal vector n, one can work out the normalized reflected and refracted rays:^[13]

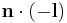$\cos\theta_1=\mathbf{n}\cdot (-\mathbf{l})$

$\cos\theta_2=\sqrt{1-\left(\frac{n_1}{n_2}\right)^2\left(1-\left(\cos\theta_1\right)^2\right)}$

$\mathbf{v}_{\mathrm{reflect}}=\mathbf{l}+\left(2\cos\theta_1\right)\mathbf{n}$

$\mathbf{v}_{\mathrm{refract}}=\left(\frac{n_1}{n_2}\right)\mathbf{l} + \left( \frac{n_1}{n_2}\cos\theta_1 - \cos\theta_2\right)\mathbf{n}$

Note: $\mathbf{n}\cdot(-\mathbf{l})$ must be positive. Otherwise, use

$\mathbf{v}_{\mathrm{refract}}=\left(\frac{n_1}{n_2}\right)\mathbf{l} + \left(\frac{n_1}{n_2}\cos\theta_1 + \cos\theta_2\right)\mathbf{n}.$

Example:

$\mathbf{l}=\{0.707107, -0.707107\},~\mathbf{n}=\{0,1\},~\frac{n_1}{n_2}=0.9$

$\mathbf{~}\cos\theta_1=0.707107,~\cos\theta_2=0.771362$

$\mathbf{v}_{\mathrm{reflect}}=\{0.707107, 0.707107\} ,~\mathbf{v}_{\mathrm{refract}}=\{0.636396, -0.771362\}$

The cosines may be recycled and used in the Fresnel equations for working out the intensity of the resulting rays.

Total internal reflection is indicated by a negative radicand in the equation for 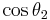$\cos\theta_2$ . In this case, an evanescent wave is produced, which rapidly decays from the surface into the second medium. Conservation of energy is maintained by the circulation of energy across the boundary, averaging to zero net energy transmission.

Dispersion

Main article: Dispersion (optics)

In many wave-propagation media, wave velocity changes with frequency or wavelength of the waves; this is true of light propagation in most transparent substances other than a vacuum. These media are called dispersive. The result is that the angles determined by Snell's law also depend on frequency or wavelength, so that a ray of mixed wavelengths, such as white light, will spread or disperse. Such dispersion of light in glass or water underlies the origin of rainbows, in which different wavelengths appear as different colors.

In optical instruments, dispersion leads to chromatic aberration; a color-dependent blurring that sometimes is the resolution-limiting effect. This was especially true in refracting telescopes, before the invention of achromatic objective lenses.

References

↑ David Michael Harland (2007). "Cassini at Saturn: Huygens results". p.1. ISBN 038726129X
↑ "Ptolemy (ca. 100-ca. 170)". Eric Weinstein's World of Scientific Biography. http://scienceworld.wolfram.com/biography/Ptolemy.html.
↑ A. I. Sabra (1981), Theories of Light from Descartes to Newton, Cambridge University Press. (cf. Pavlos Mihas, Use of History in Developing ideas of refraction, lenses and rainbow, p. 5, Demokritus University, Thrace, Greece.)
↑ William Whewell, History of the Inductive Science from the Earliest to the Present Times, London: John H. Parker, 1837.
↑ Wolf, K. B. (1995), "Geometry and dynamics in refracting systems", European Journal of Physics 16: 14–20.
↑ Rashed, Roshdi (1990). "A pioneer in anaclastics: Ibn Sahl on burning mirrors and lenses". Isis 81: 464–491. doi:10.1086/355456.
↑ Sara Cerantola, "La ley física de Ibn Sahl: estudio y traducción parcial de su Kitāb al-ḥarraqāt / The physics law of Ibn Sahl: Study and partial translation of his Kitāb al-ḥarraqāt", Anaquel de Estudios Árabes, 15 (2004): 57-95.
↑ Kwan, A., Dudley, J., and Lantz, E. (2002). "Who really discovered Snell's law?". Physics World 15 (4): 64. http://physicsworldarchive.iop.org/index.cfm?action=summary&doc=15%2F4%2Fphwv15i4a44%40pwa-xml&qt=.
↑ Fokko Jan Dijksterhuis (2004). Lenses and Waves: Christiaan Huygens and the Mathematical Science of Optics in the Seventeenth Century. Springer. ISBN 1402026978. http://books.google.com/?id=cPFevyomPUIC&pg=PA135&lpg=PA135&dq=Descartes-had-seen-Snel%27s+intitle:Lenses+intitle:and+intitle:Waves+intitle:Christiaan.
↑ George Sarton (1955). The Appreciation of Ancient and Medieval Science During the Renaissance. University of Pennsylvania Press. xiii. http://books.google.com/?id=q9oZAAAAMAAJ&q=snell+snel+snellius&dq=snell+snel+snellius.
↑ Snell's Law
↑ John D Joannopoulos, Johnson SG, Winn JN & Meade RD (2008). Photonic Crystals: Molding the Flow of Light (2^nd ed.). Princeton NJ: Princeton University Press. ISBN 978-0-691-12456-8. http://ab-initio.mit.edu/book/.
↑ Andrew S. Glassner (1989). An Introduction to Ray Tracing. Morgan Kaufmann. ISBN 0122861604. http://books.google.com/?id=YPblYyLqBM4C.

External links

Discovery of the law of refraction
Snell's Law of Refraction (Wave Fronts) by Todd Rowland, Wolfram Demonstrations Project.